X
Pornstars
 Anal
Anal 60 FPS
60 FPS Teen
Teen Big Tits
Big Tits Japanese
Japanese POV
POV Asian
Asian Amateur
Amateur Masturbation
Masturbation Lesbian
Lesbian Milf
Milf Threesome
Threesome Interracial
Interracial Mature
Mature Creampie
Creampie Blowjob
Blowjob Big Ass
Big Ass Hardcore
Hardcore Group Sex
Group Sex Pornstar
Pornstar Ebony
Ebony Shemale
Shemale Big Dick
Big Dick Homemade
Homemade Double Penetration
Double Penetration Blonde
Blonde HD Sex
HD Sex Toys
Toys Lingerie
Lingerie BBW
BBW Webcam
Webcam Cumshot
Cumshot Latina
Latina Massage
Massage Brunette
Brunette Squirt
Squirt Public
Public BDSM
BDSM Students
Students Striptease
Striptease Petite
Petite Orgy
Orgy Handjob
Handjob Indian
Indian Outdoor
Outdoor Redhead
Redhead Gay
Gay Small Tits
Small Tits Footjob
Footjob Older Men
Older Men Fetish
Fetish Hentai
Hentai Housewives
Housewives Fat
Fat Swinger
Swinger Uniform
Uniform Office
Office Bondage
Bondage Doctor
Doctor Spy Cams
Spy Cams For Women
For Women Bukkake
Bukkake HQ Porn
HQ Porn Vintage
Vintage Fisting
Fisting Bisexual
Bisexual Sleep
Sleep Hotel
Hotel Nurses
Nurses VR Porn
VR Porn





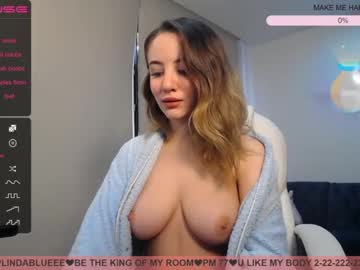


































 Deepthroat mamada de Grande tetas masaje chica 255 min
Deepthroat mamada de Grande tetas masaje chica 255 min With Big Juggs Banged In Of....jpg?v=0.8) Hot Girl (lisa ann) With Big Juggs Banged In Of...5 min
Hot Girl (lisa ann) With Big Juggs Banged In Of...5 min Sex In Office With Big Melon Jugg....jpg?v=0.8) (krissy lynn) Sex In Office With Big Melon Jugg...5 min
(krissy lynn) Sex In Office With Big Melon Jugg...5 min Big Boobs Banged Hardc....jpg?v=0.8) Hot Girl (madison scott) Big Boobs Banged Hardc...5 min
Hot Girl (madison scott) Big Boobs Banged Hardc...5 min Sexy chica da Grande tetas lesbianas un orgasmo 255 min
Sexy chica da Grande tetas lesbianas un orgasmo 255 min Pequeña chica le da grandes tetas a lesbiana un orgasmo inolvidable 255 min
Pequeña chica le da grandes tetas a lesbiana un orgasmo inolvidable 255 min Get Hardcore A....jpg?v=0.8) Wet Big Ass Girl (phoenix marie) Get Hardcore A...5 min
Wet Big Ass Girl (phoenix marie) Get Hardcore A...5 min Get Har....jpg?v=0.8) Big Round Boobs Girl (mercedes carrera) Get Har...6 min
Big Round Boobs Girl (mercedes carrera) Get Har...6 min Grande curvas a tope chica obtener su culo clavado profundo película5 min
Grande curvas a tope chica obtener su culo clavado profundo película5 min Sexy Big Tits Office Girl Love....jpg?v=0.8) (Missy Martinez) Sexy Big Tits Office Girl Love...7 min
(Missy Martinez) Sexy Big Tits Office Girl Love...7 min como anal duro estilo bang video-25.jpg?v=0.8) Grande mojado aceitado culo chica (rachael madori) como anal duro estilo bang video-257 min
Grande mojado aceitado culo chica (rachael madori) como anal duro estilo bang video-257 min Sex In Office With Big Juggs Sluty Girl (Phoeni...7 min
Sex In Office With Big Juggs Sluty Girl (Phoeni...7 min Hard Banged In Office A Real Slut Big Tits Girl...8 min
Hard Banged In Office A Real Slut Big Tits Girl...8 min In Hard Ana....jpg?v=0.8) Gorgeous Big Ass Girl (rose monroe) In Hard Ana...6 min
Gorgeous Big Ass Girl (rose monroe) In Hard Ana...6 min Hard Style Sex In Office With Sluty Big Tits Gi...7 min
Hard Style Sex In Office With Sluty Big Tits Gi...7 min clip-25.jpg?v=0.8) Sexo con puta trabajadora Big Juggs Office Girl (lezley zen) clip-255 min
Sexo con puta trabajadora Big Juggs Office Girl (lezley zen) clip-255 min Hardcore Sex With Sluty Big Round Boobs Office ...7 min
Hardcore Sex With Sluty Big Round Boobs Office ...7 min con grandes tetas disfrutar de sexo vid-25.jpg?v=0.8) Oficina puta chica (estilos nadia) con grandes tetas disfrutar de sexo vid-255 min
Oficina puta chica (estilos nadia) con grandes tetas disfrutar de sexo vid-255 min Anal Hardcore Sex With Big Wet Oiled Butt Girl ...5 min
Anal Hardcore Sex With Big Wet Oiled Butt Girl ...5 min Hard Banged In Offi....jpg?v=0.8) Big Melon Tits Girl ( elle) Hard Banged In Offi...5 min
Big Melon Tits Girl ( elle) Hard Banged In Offi...5 min Caliente chica rachael madori con gran culo redondo obtener anal tener relaciones sexuales mov-255 min
Caliente chica rachael madori con gran culo redondo obtener anal tener relaciones sexuales mov-255 min Hard Bang In Office With Big Tits Horny Sluty G...7 min
Hard Bang In Office With Big Tits Horny Sluty G...7 min Hardcore Anal Sex With Beauty Curvy Big Butt Gi...7 min
Hardcore Anal Sex With Beauty Curvy Big Butt Gi...7 min Tómelo profundamente en su detrás clip-25.jpg?v=0.8) Big Butt Girl (rachael madori) Tómelo profundamente en su detrás clip-255 min
Big Butt Girl (rachael madori) Tómelo profundamente en su detrás clip-255 min Chica caliente con grandes tetas el amor de tener relaciones sexuales en la película de la oficina-25.jpg?v=0.8) (Rachel RoXXX) Chica caliente con grandes tetas el amor de tener relaciones sexuales en la película de la oficina-257 min
(Rachel RoXXX) Chica caliente con grandes tetas el amor de tener relaciones sexuales en la película de la oficina-257 min With Big Cock In Her....jpg?v=0.8) Big Ass Girl (rose monroe) With Big Cock In Her...5 min
Big Ass Girl (rose monroe) With Big Cock In Her...5 min Lynna Nilsson Tetas Grandes Oficina Puta Chica Obtener Estilo Duro Clavado Video-256 min
Lynna Nilsson Tetas Grandes Oficina Puta Chica Obtener Estilo Duro Clavado Video-256 min With Big Tits Banged Hard Style video-25.jpg?v=0.8) Office Girl (lou lou) With Big Tits Banged Hard Style video-255 min
Office Girl (lou lou) With Big Tits Banged Hard Style video-255 min 25 cm vs chicas negras34 min
25 cm vs chicas negras34 min CHICA SQUIRT 255 min
CHICA SQUIRT 255 min Enjoy Anal Sex On Camera video-25.jpg?v=0.8) Big Round Ass Girl (samia duarte) Enjoy Anal Sex On Camera video-256 min
Big Round Ass Girl (samia duarte) Enjoy Anal Sex On Camera video-256 min mov-25.jpg?v=0.8) Sexo duro en la oficina con una chica de grandes tetas redondas (lynna nilsson) mov-257 min
Sexo duro en la oficina con una chica de grandes tetas redondas (lynna nilsson) mov-257 min Puta Grande melón tetas chica tener Sexo en oficina vid5 min
Puta Grande melón tetas chica tener Sexo en oficina vid5 min Hardcore Sexo escena con Grande delicioso culo chica clip5 min
Hardcore Sexo escena con Grande delicioso culo chica clip5 min Aceitado todo hasta Grande trasero chica tomarlo en su culo clip5 min
Aceitado todo hasta Grande trasero chica tomarlo en su culo clip5 min Hard Sex On Cam In Office With Big Juggs Gorgeo...7 min
Hard Sex On Cam In Office With Big Juggs Gorgeo...7 min Verified model8 min
Verified model8 min Hermosa chica nikki benz con delicioso gran culo obtener anal vid5 min
Hermosa chica nikki benz con delicioso gran culo obtener anal vid5 min Hermosa chica follada Duro por Grande negro dick 255 min
Hermosa chica follada Duro por Grande negro dick 255 min Chorros goth girl necesita más cum 255 min
Chorros goth girl necesita más cum 255 min Puta Grande juggs chica obtener salvaje en oficina Sexo cinta clip5 min
Puta Grande juggs chica obtener salvaje en oficina Sexo cinta clip5 min Take It Dee....jpg?v=0.8) Luscious Big Ass Girl (rose monroe) Take It Dee...6 min
Luscious Big Ass Girl (rose monroe) Take It Dee...6 min Nikki benz7 min
Nikki benz7 min Long Fuck a Girl y ella se corre intensamente - Orgasms 255 min
Long Fuck a Girl y ella se corre intensamente - Orgasms 255 min vid-25.jpg?v=0.8) Cinta de sexo anal con una chica aceitada de gran culo con curvas (alex tori) vid-255 min
Cinta de sexo anal con una chica aceitada de gran culo con curvas (alex tori) vid-255 min gran culo engrasado chica disfruta de sexo anal profundo y duro mov-25.jpg?v=0.8) (sarah vandella) gran culo engrasado chica disfruta de sexo anal profundo y duro mov-258 min
(sarah vandella) gran culo engrasado chica disfruta de sexo anal profundo y duro mov-258 min Aceitado Grande culo chica tenerlo en cam en su detrás vid5 min
Aceitado Grande culo chica tenerlo en cam en su detrás vid5 min Cinta de sexo anal con caliente y mojado gran culo chica clip5 min
Cinta de sexo anal con caliente y mojado gran culo chica clip5 min Slut Big Tits Office Girl Like ....jpg?v=0.8) (madison scott) Slut Big Tits Office Girl Like ...7 min
(madison scott) Slut Big Tits Office Girl Like ...7 min samia duarte grande mojado culo chica en Hardcore anal tener relaciones sexuales vid6 min
samia duarte grande mojado culo chica en Hardcore anal tener relaciones sexuales vid6 min video-25.jpg?v=0.8) Anal Hardcore Sexo con Caliente Puta Gran Culo Aceitado Chica (Kat Dior) video-257 min
Anal Hardcore Sexo con Caliente Puta Gran Culo Aceitado Chica (Kat Dior) video-257 min Grande a tope hermosa chica obtener su detrás clavado clip5 min
Grande a tope hermosa chica obtener su detrás clavado clip5 min Chico caliente se folla a una chica blanca desde el capó 255 min
Chico caliente se folla a una chica blanca desde el capó 255 min Bang Deep In Ass On Cam A Slut Curvy Big Butt G...5 min
Bang Deep In Ass On Cam A Slut Curvy Big Butt G...5 min Slut Girl With Big Round Ass Like Deep Anal Sex movie-25.jpg?v=0.8) (rachael madori) Slut Girl With Big Round Ass Like Deep Anal Sex movie-257 min
(rachael madori) Slut Girl With Big Round Ass Like Deep Anal Sex movie-257 min en escena de sexo en la oficina clip-25.jpg?v=0.8) Round Big Boobs Girl (lou lou) en escena de sexo en la oficina clip-257 min
Round Big Boobs Girl (lou lou) en escena de sexo en la oficina clip-257 min movie-25.jpg?v=0.8) Deep Anal Intercorse With Naughty Big Oiled Butt Girl (Nikki Benz) movie-257 min
Deep Anal Intercorse With Naughty Big Oiled Butt Girl (Nikki Benz) movie-257 min